Методика реализации внутри- и межпонятийных связей

Ошибки, допущенные при распознавании объектов в указанных выше вопросах, обусловлены тем, что во всех случаях нет сведений о некоторых необходимых признаках, а школьники испытывают большие трудности при распознавании объектов в задачах с неопределенным составом условий.

Для того чтобы учащиеся могли верно подводить объект под понятие в случаях конъюнктивной и дизъюнктивной структур определений, можно вместе с ними составить следующую схему распознавания.

1. Исходя из условий выбрать удобное определение понятия, под которое подводится объект.

2. Выделить в выбранном определении все признаки понятия.

3. Установить, какими логическими союзами связаны между собой эти признаки.

4. Если все признаки понятия связаны союзом «и», то для подведения объекта под понятие надо проверить последовательно выполнение для данного объекта всех признаков, если не выполнен хотя бы один признак, то объект не принадлежит к указанному понятию, если же все признаки выполнены, то объект принадлежит объему этого понятия.

5. Если все признаки понятия связаны союзом «или», то для установления принадлежности объекта объему понятия достаточно проверить выполнение хотя бы одного из этих признаков.

Систематическое, целенаправленное использование такой схемы распознавания объекта позволит избежать ошибок, допускаемых учащимися при осуществлении логического приема мышления — подведения объекта под понятие.

Рассмотрим еще один вопрос, связанный с определением понятий.

Радикальное изменение содержания школьной математики привело в свое время к усилению строгости изложения курса. Отражением этого явилось усиленное внимание к строгости определений понятий, изучаемых в курсе математики. В большей степени дефиниционный формализм коснулся содержания основ математического анализа, изучаемых в школе.

Наличие большого числа строгих определений понятий в прежнем курсе алгебры и начал анализа привело к смещению в преподавании акцента от интуитивного к логическому. В таком случае в процессе обучения отрабатывались и закреплялись формальные определения понятий вместо выработки у учащихся адекватных представлений о понятиях, необходимых для правильного их использования в практической работе.

Такое изменение методической ситуации в изучении понятий привело к формализму в знаниях учащихся. Приведем примеры.

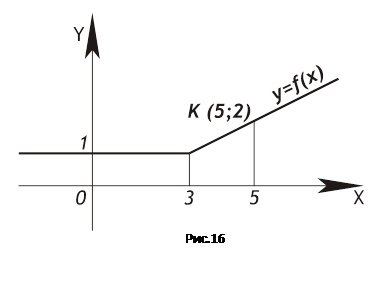
Учащимся предлагается задание: «Вычислить (x)dx, если функция f(x) задана графиком (рис. 16)». Немногие учащиеся решат ее рационально, не вычисляя интеграла, а находя сумму площадей прямоугольника и трапеции.

Предупредить формализм в знаниях учащихся возможно за счет усиления связей интуитивно-опытных представлений с логической формализацией, а также за счет усиления наглядно-смысловой стороны изучаемых вопросов.

Использование и оперирование графическими моделями понятий математического анализа есть эффективное средство преодоления и предупреждения формализма в знаниях, повышения прочности и осознанности знаний, развития должной интуиции у учащихся в понимании фундаментальных понятий и внутрипонятийных связей. Геометрический язык позволяет проводить пропедевтику основных понятий математического анализа, способствует формированию политехнических знаний и прикладных умений, содействует развитию у учащихся навыков моделирования явлений действительности. Результаты могут быть достигнуты без дополнительных затрат учебного времени. С этой целью задачи графического содержания достаточно использовать в качестве устных вопросов к традиционным вопросам курса.