Методика реализации внутри- и межпонятийных связей

Покажем, каким образом геометрическое истолкование понятия производной может способствовать правильному построению графиков функции с помощью дифференциального исчисления. (Мы проиллюстрируем тем самым реализацию внутрипредметных связей на уровне умений и навыков.)

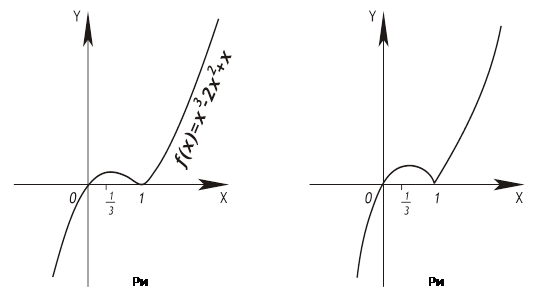
1. График функции f (х) = х3 -2х2 + х должен быть таким, каким он изображен на рисунке 17. Учащиеся же представляют его в виде, изображенном на рисунке 18.

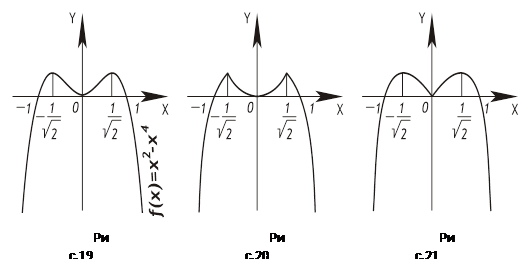
2. Функция f(х)=х2—х4 должна иметь график, изображенный на рисунке 23, а школьники строят ошибочно другие эскизы графика (рис. 19,20)

Эти ошибки происходят из-за того, что школьники при построении графика функции берут во внимание лишь характер монотонности функции и то, какой экстремум имеет функция в той или иной экстремальной точке, забывая при этом учесть, существует ли производная функции в этих точках, и если да, то каково ее значение.

Действительно, график функции f(x)=x2—x4 (см. рис. 20) построен так, что в точках с абсциссами х=— и х= к кривой нельзя провести касательных, в то время как производная функции в этих точках существует (она равна нулю), а значит, проведение касательных возможно.

Следовательно, при построении графика функции школьники должны уметь сопоставить ход кривой в окрестностях экстремальных точек с тем, возможно ли проведение касательных или нет, причем в случае равенства нулю производной функции в этих точках касательные должны быть параллельны оси х.

3. Пусть нужно построить график функции f(x)=x4 — 2х2 — 3. Учащиеся оформляют проведенное исследование функции в виде таблицы.

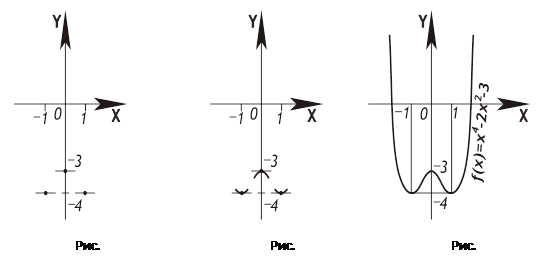
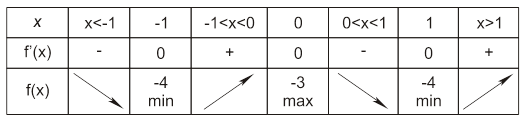
До построения графика функции полезно сначала на координатной плоскости отметить точки (—1; —4), (0; —3), (1; —4) (рис. 22)

Учитывая, что касательные к графику функции в этих экстремальных точках параллельны оси х (это следует из равенства нулю угловых коэффициентов, так как f' (—1) = f'(0) = f'(1) = 0), проведем в этих точках прямые, параллельные оси х (рис. 22). Затем следует, согласно таблице, наметить ход кривой в точках (рис.23). Построение самого же графика функции явится завершающим этапом (рис. 24).

Внутрипонятийные связи играют ведущую роль в образовании понятий а межпонятийные связи — в его формировании.

Формирование понятия более длительный процесс, чем его образование. Образование понятия связано с изучением овладения его содержанием, а формирование понятия характеризуется еще и овладением его объемом.

Содержательной стороной межпонятийных связей являются логические отношения, которые устанавливаются между понятиями. Остановимся на их характеристике. Дадим каждому из видов отношений соответствующее определение.

К основным отношениям между понятиями следует отнести: отношение тождества, отношение несогласованности, отношение подчинения, отношение соподчинения, отношение частичного совпадения. Эти отношения определяют структуру понятийного аппарата курса математики.

Определение 1. Понятия А и В тождественны, если полностью совпадают их объемы (рис. 25)