Методика реализации внутри- и межпонятийных связей

Каждая ошибка характеризуется содержанием и причинами возникновения. Содержание ошибки лежит на поверхности явления, а причина скрыта в глубине его.

Математические ошибки подразделяются на случайные и систематические (устойчивые). К случайным ошибкам относятся те, которые появляются однократно, несистематически у одного-двух учащихся класса. К устойчивым ошибкам относят либо те, которые появляются у одного и того же ученика (или нескольких) неоднократно, либо наблюдаются, хотя и однократно, но у многих учащихся.

Причины устойчивых ошибок учащихся являются следствием:

а) психологических факторов (ослабление внимания, памяти, мышления);

б) несовершенства организации процесса обучения;

в) недостатков программ, учебников по математике.

В педагогической литературе правомерно ставятся вопросы:

«Нужно ли предупреждать ошибки в действиях учащихся?»;

«Нужно ли допущенную ошибку обсуждать фронтально или же целесообразнее это сделать индивидуально?»;

«Есть ли ошибки такого рода, обсуждение которых вообще нецелесообразно?».

Но продуманная работа над систематическими (устойчивыми) ошибками может оказаться эффективным средством формирования сознательных и прочных знаний учащихся. В каждом конкретном случае учитель должен сам определить, какая форма работы будет целесообразнее: фронтальная или индивидуальная.

Большое значение в работе с внутрипонятийными связями играют контрпримеры, которые вначале, приводятся учителем, а затем к их конструированию подключаются и учащиеся.

Так, для определения а) и б) данных при описании типичных ошибок четвертого вида можно соответственно привести контр.пример, иллюстрирующий их ошибочность:

а) Число 12 делится на себя и на единицу, но оно не является простым числом.

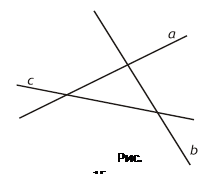
б) Прямые а, b, с (рис. 15) лежат в одной плоскости, не имеют ни одной общей точки, но не являются параллельными.

Подобного рода работа повысит математическую культуру учащихся, научит их сознательно относиться к каждому слову в определении.

Контр. примеры чаще всего применяются тогда, когда надо убедить ученика в том, что он ошибается. Полезно уже на уровне 5-6 классов предлагать задания следующего содержания: «Приведите контр.примеры, доказывающие ложность следующих высказываний:

а) любые три отрезка могут быть сторонами треугольника;

б) сумма любого четного и любого нечетного числа есть число простое

в) любая фигура, имеющая три угла, является треугольником;

Успешному усвоению внутрипонятийных связей будет способствовать организация активной познавательной деятельности школьников на всех этапах формирования понятия. Покажем, как можно это сделать на примерах.

1. Для формирования понятия медианы треугольника учащимся предлагается:

а) построить произвольный треугольник;

б) соединить отрезком его вершину с серединой противоположной стороны.

После этой работы учитель говорит: «Такой отрезок называется медианой треугольника» — и предлагает учащимся самим сформулировать определение медианы треугольника.

2. Работая над понятием квадратное уравнение, полезно предложить учащимся заполнить таблицу 1.

Таблица 1