Методика реализации внутри- и межпонятийных связей

В данной группе задач исключено беспорядочное варьирование коэффициента, при котором ученик может упустить необходимые для обобщения связи между коэффициентом k и свойствами функции y = kx. Все задачи направлены на осознанное понимание учащимися двух различных факторов, определяющих свойства функции: абсолютная величина k, знак коэффициента k.

Организуя работу над внутрипонятийными связями, учителю следует иметь в виду, что при этом важно варьировать несущественные признаки понятия. Особое значение эта работа имеет при формировании геометрических понятий. Если учитель ограничивается, например, стандартными чертежами, то школьники достаточно быстро связывают формируемое понятие с фигурами определенного вида и расположения.

Ведь использование стандартного чертежа вызывает у учащегося неверные ассоциации, в результате чего он в содержание понятия вносит и частные признаки демонстрируемой фигуры. В такой ситуации наблюдается разобщенность между словесным объяснением учителя и наглядной интерпретацией. Это приводит к тому, что знания, формируемые на базе одного и другого, не соответствуют друг другу.

Приведем несколько примеров, подтверждающих сказанное.

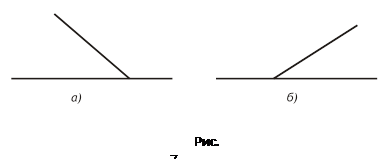
1. Учащиеся при выполнении задания на распознавание фигур, например, к углу относили лишь фигуру, изображенную на рисунке 6б. Причиной послужило то, что учитель, формируя понятие угла, использовал лишь рисунки, подобные рисунку 6б, и школьники с бедными геометрическими представлениями попали «в плен» к наглядности.

2.Некоторые учащиеся к смежным углам отнесли лишь углы, изображенные на рисунке 7б.

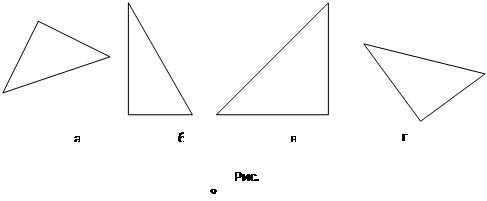
3. Многие ученики к прямоугольным треугольникам относят лишь те, у которых прямой угол находится «внизу» (рис. 8 б, в). Причиной ошибочного представления о понятии явилось то, что учащиеся при его введении пользовались лишь одним признаком, а не совокупностью существенных признаков, при этом доминирующим стал наиболее ярко выраженный несущественный признак.

Следует иметь в виду, что формирование понятия в сознании учащихся в значительной степени зависит от того, в каком виде произошло первое знакомство с этим понятием.

Не менее важным в работе над внутрипонятийными связями является формирование у школьников умения переосмысливать фигуру в плане другого понятия, вычленять и комбинировать из элементов изображения новые фигуры, не указанные в условии задачи. Проиллюстрируем сказанное на примерах.

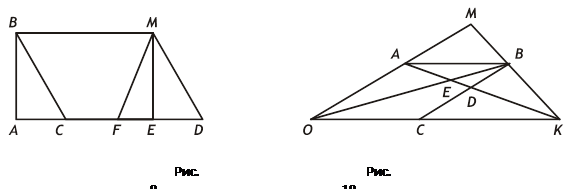
1. Назовите все четырехугольники, изображенные на рисунке 9.

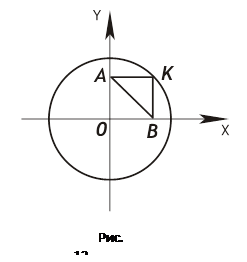
2. В какие фигуры входит отрезок АВ на рисунке 10?

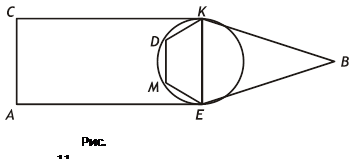
3 Чем является отрезок КЕ на рисунке 11?

Радиус окружности равен 5 см (рис. 10).

Найдите длину отрезка АВ. Для решения задачи учащиеся должны увидеть радиус окружности в качестве диагонали ОК прямоугольника АКВО. Тогда на основе равенства диагоналей прямоугольника они получат, что АВ = 5 см.

Для того чтобы учащиеся понимали роль и назначение чертежа, умели читать и строить его по словесному заданию условия, целесообразно довести школьников до полного понимания роли чертежа в геометрии;