Методическое обеспечение изучения комплексных чисел в 10 классе общеобразовательной школы

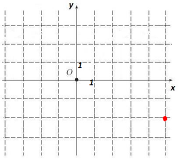
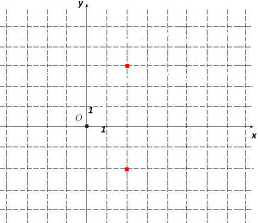
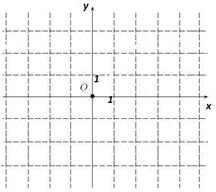
рис. 1

А4. Какому числу соответствует точка на рис. 1?

а)

b)

c)

d)

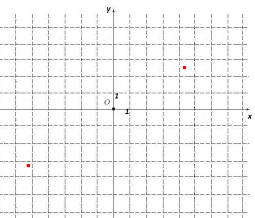
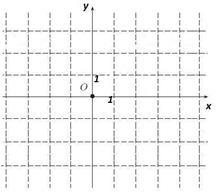
А5. Какому числу соответствует точка на рис. 2?

а)

b)

c)

d)

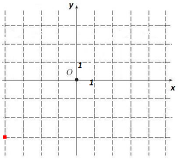
рис. 2

А6. Выберите чертеж, на котором правильно изображены числа , если .

1 b) 2 c) 3 d)4

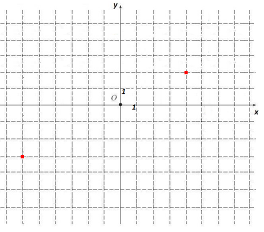
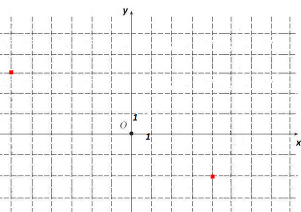1) 2)

3) 4)

Часть В

В1. Изобразите на координатной плоскости множество всех комплексных чисел, у которых:

а) действительная часть равна -3 b) мнимая часть равна 1.

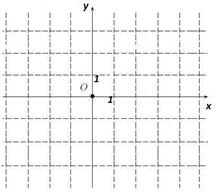
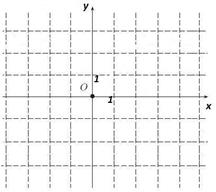
c) отношение мнимой части d) сумма квадратов действительной

к действительной равно -2 и мнимой части равна 4.

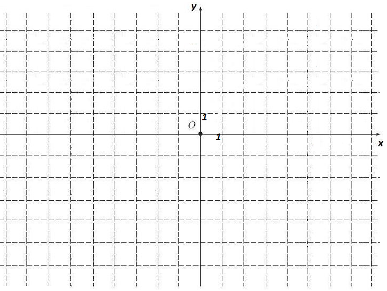
В2. Для комплексных чисел и изобразите на координатной плоскости числа:

а) б) в) г)

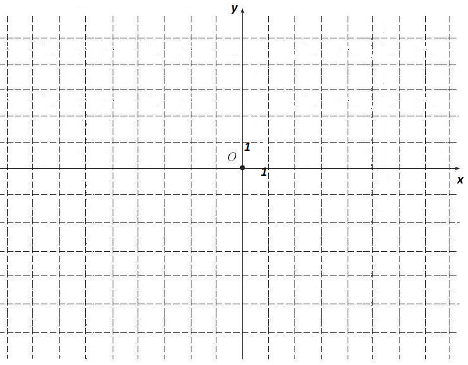
В3. Для комплексного числа изобразить на координатной плоскости числа

а) б) в)

В4. Вставьте пропущенные слова:

Геометрически операция сопряжения есть …………………………………… относительно оси ………………………. .

Часть С

С1. Обоснуйте геометрически свойство:

С2. Обоснуйте геометрически свойство:

§34. Тригонометрическая форма записи комплексного числа

§34 самый большой по объему, количеству теорем и по числу крайне важных понятий. В этом параграфе соединяются вместе и алгебраические и геометрические представления о комплексных числах. Разбираются такие понятия, как модуль, аргумент комплексного числа, умножение и деление комплексных чисел. Изучаются переход от алгебраической к тригонометрической форме записи комплексного числа, умножение и деление чисел в тригонометрической форме.

Тест №3 по теме

«Тригонометрическая форма записи комплексного числа»

Часть А

А1. Вычислите , если

а) b) c) d)

A2. Геометрически модуль комплексного числа – это

а) расстояние от до

b) расстояние от точки координатной плоскости, соответствующей числу , до начала координат

c) расстояние от точки координатной плоскости, соответствующей числу , до оси абсцисс