Способы описания алгоритмов

Рассмотрим три способа описания алгоритмов:

словесно-формульный (на естественном языке с использованием математических формул);

графический (блок-схема);

на языке программирования (программа).

Для наглядности рассмотрим пример решения квадратного уравнения с помощью всех трёх способов.

1 способ: словесно-формульный.

Пусть дано квадратное уравнение a*x2 + b*x + c = 0.

Напишем алгоритм решения этого уравнения.

Начало.

Ввод A, B, C.

D = B2 - 4 A C.

Если D < 0, то идти к п.6.

Если D > 0, то идти к п.8.

Действительных корней нет.

Идти к п.10.

X1 = ( - B - ) / 2 А; X2 = ( - B +) / 2 A.

Вывести значения X1 и X2.

Конец.

2 способ: графический (блок-схемный).

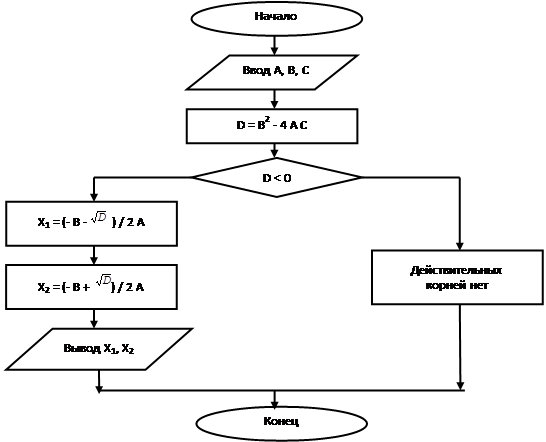
При блок-схемном описании алгоритм изображается геометрическими фигурами (блоками), связанными по управлению линиями (направлениями потока) со стрелками. В блоках записывается последовательность действий.

Данный способ по сравнению с другими способами записи алгоритма имеет ряд преимуществ. Он наиболее нагляден: каждая операция вычислительного процесса изображается отдельной геометрической фигурой. Кроме того, графическое изображение алгоритма наглядно показывает разветвления путей решения задачи в зависимости от различных условий, повторение отдельных этапов вычислительного процесса и другие детали.

Оформление в графическом описании должно соответствовать определенным требованиям.

Линии, соединяющие блоки и указывающие последовательность связей между ними, должны проводится параллельно линиям рамки. Стрелка в конце линии может не ставиться, если линия направлена слева направо или сверху вниз. В блок может входить несколько линий, то есть блок может являться преемником любого числа блоков. Из блока (кроме логического) может выходить только одна линия. Логический блок может иметь в качестве продолжения один из двух блоков, и из него выходят две линии. Если на схеме имеет место слияние линий, то место пересечения выделяется точкой. В случае, когда одна линия подходит к другой и слияние их явно выражено, точку можно не ставить.

Схему алгоритма следует выполнять как единое целое, однако в случае необходимости допускается обрывать линии, соединяющие блоки.

Если при обрыве линии продолжение схемы находится на этом же листе, то на одном и другом конце линии изображается специальный символ соединитель - окружность диаметром 0,5 а. Внутри парных окружностей указывается один и тот же идентификатор. В качестве идентификатора, как правило, используется порядковый номер блока, к которому направлена соединительная линия.

Если схема занимает более одного листа, то в случае разрыва линии вместо окружности используется межстраничный соединитель. Внутри каждого, соединителя указывается адрес - откуда и куда направлена соединительная линия. Адрес записывается в две строки: в первой указывается номер листа, во второй - порядковый номер блока .

Блок-схема должна содержать все разветвления, циклы и обращения к подпрограммам, содержащиеся в программе.