Обобщающее повторение как средство реализации внутрипредметных связей

Рассмотрим решение задачи, которая может быть предложена учащимся.

Докажите, что для всех неотрицательных х справедливо неравенство:

Рассмотрим функцию

на промежутке [0;¥).

Найдём производную этой функции:

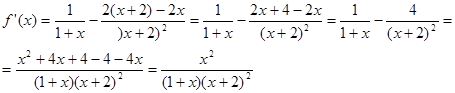
При любом значении х >0 справедливо неравенство f (х)>0. Это значит, что на промежутке (0;+¥) функция f(x) возрастает. В то же время замечаем, что функция f(x) на промежутке х>0 есть непрерывная функция, как сумма непрерывных функций. А это значит, что она на левом конце этого промежутка при х=0 принимает своё наименьшее значение.

А так как

то для любого х³0 f(x)³0, т.е.

откуда

Рассмотрим ещё один пример обобщающего повторения на уровне теорий.

Обобщая материал о применении производной к приближённым вычислениям, можно показать учащимся идею линеаризации функции. Суть этой идеи состоит в следующем.

В случае непрерывности функции у=f(x) в некоторой точке х0 её значения для всех значений аргумента из достаточно малой окрестности точки х0 приближённо равны значению f(x0). Если же к свойству непрерывности функции в точке х0 добавить ещё одно свойство, а именно её дифференцируемость в этой точке, то значения функции y=f(x) в достаточно малой окрестности точки х0 приближённо могут быть заменены значениями некоторой линейной функции y=kx+b (как впоследствии будет выяснено, это уравнение есть уравнение касательной к кривой y=f(x), проведённой к ней в точке с абциссой х0).

Фактически это следует из разложения функции в ряд Тейлора. Действительно, пусть мы имеем разложение

Если бы функция f(x) в точке x0 обладала лишь свойством непрерывности в точке x0, то мы имели бы приближённое равенство f(x)»f(x0).

Если же функция f(x) в точке x0 имеет первую производную, то приближение будет более точным; к правой части равенства f(x)=f(x0) добавится ещё одно слагаемое

т.е. имеет место приближённое равенство:

При наличии второй производной функции f(x) в точке х0 будем иметь

Следовательно, если функция бесконечно дифференцируема, то приближение может быть сделано с любой степенью точности.

Однако в курсе алгебры и начал анализа рассматривается лишь понятие первой производной. Поэтому при изучении применений производной к приближённым вычислениям ограничиваются лишь двумя первыми слагаемыми ряда Тейлора, т.е. используют приближённое равенство:

Обобщение формулы

на уровне идеи аппроксимации даёт представление о решении этих вопросов. Если функция имеет производные любого порядка, то её можно приблизить многочленом с какой угодно точностью. Так получаются ряды для функций

sin х , cos x , е х , 1n x .

Геометрически это означает, что график функции n-раз, дифференцируемой в точке х0, вблизи этой точки можно приближённо считать графиком некоторого многочлена n-ой степени.

Конечно, в школьном курсе нет возможности рассматривать с учащимися этот вопрос в таком общем плане. Но внимание к постановке задачи, отдельные примеры не только расширяют кругозор учащихся, но и помогут преодолеть некоторые методические трудности.

Одной из таких трудностей, как показал опыт, является переход от равенства

к равенству

Возникновение этой трудности можно предотвратить уже при постановке проблемы, если начать изложение примерно таким пояснением: «Вы знаете, что для функции f(x), непрерывной в точке х0, выполняется равенство