Обобщающее повторение как средство реализации внутрипредметных связей

Приведем примеры знаний, которые можно использовать при обобщающем повторении на уровне понятий в различных темах школьного курса математики.

1. При обобщении темы «Многогранники» курса геометрии 11 класса учащимся может быть предложено такое задание.

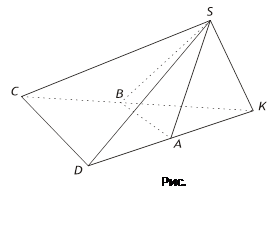
Существует ли четырехугольная пирамида, две противоположные грани которой перпендикулярны основанию пирамиды?

Ответом может служить рисунок 34. В пирамиде SABCD грани SBC и SAD перпендикулярны основанию ABCD. (Искомая пирамида получена из треугольной пирамиды SKCD, у которой грани SCK и SDK перпендикулярны основанию - KCD.)

Для проведения обобщающего повторения по теме „Производная" можно повторить определение производной, алгоритм нахождения производной функции по определению, основные правила и формулы, связанные с производной.

2. Для того чтобы обучить учащихся различать свойства и признаки понятий, полезной при организации обобщающего повторения на уровне понятий окажется работа по переформулированию теорем в условной форме: «Если ., то .».

Действительно, как узнать о свойстве или о признаке идет речь в теореме? На этот вопрос легко ответить, если теорему сформулировать в условной форме. Если окажется, что рассматриваемое понятие находится в условии теоремы, то теорема выражает свойство этого понятия, если же понятие окажется в заключение теоремы, то она выражает признак. Покажем на примерах.

a) Теорема Пифагора: «В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов». Переформулируем теорему из категорической формы в условную. Будем иметь: «Если треугольник прямоугольный, то квадрат гипотенузы равен сумме квадратов катетов». Так как понятие прямоугольный треугольник оказалось в условии теоремы, то теорема выражает собой свойство этого понятия.

b) Теорема: «Треугольник, у которого углы при основании равны, равнобедренный». Сформулируем теорему в терминах «если ., то .». Будем иметь: «Если в треугольнике углы при основании равны, то треугольник равнобедренный». Так как понятие равнобедренный треугольник оказалось в заключение теоремы, то эта теорема выражает собой признак.

Заметим, что некоторые теоремы одновременно выражают как свойство, так и признак одного и того же понятия. Так обстоит дело в последнем случае; сформулировать теорему в виде: «Если треугольник равнобедренный, то углы при основании равны», мы имели бы свойства равнобедренного треугольника.

2. Обобщающее повторение на уровне системы понятий.

Обобщающее повторение на уровне системы понятий преследует цель выработать у учащихся умение сопоставлять изученные понятия, отыскивать новые связи и отношения между ними, прослеживать развитие понятий в их иерархических зависимостях, т.е. устанавливать подчиненность вида роду в случае сопоставимых понятий. При этом происходит либо обогащение и расширение ранее изученных понятий.

Если на уровне понятий обобщающее повторение организовывалось с помощью методов наблюдения и сравнения, то на уровне системы понятий на первый план выдвигается анализ взаимосвязей понятий. Это дает возможность классифицировать понятия не только по их природе, но, что еще более существенно, по отношениям между ними.

Обобщающее повторение на уровне системы понятий предлагает такую ориентацию учащихся в учебном материале, которая бы позволяла определить и усвоить общий способ преобразования этого материала на основе соответствующих предметных и знаковых моделей. К таким знаковым моделям относятся классификационные схемы, сводные таблицы, определенные записи, опорные конспекты. Они позволяют придать полученным при обобщающем повторении систематизированным знаниям определенную структуру.

Покажем на примерах, как может быть организовано обобщающее повторение на уровне системы понятий.

1. В теме «Сумма углов треугольника» курса геометрии 7 класса центральными являются признаки и свойства параллельных прямых, теорема о сумме углов треугольника.

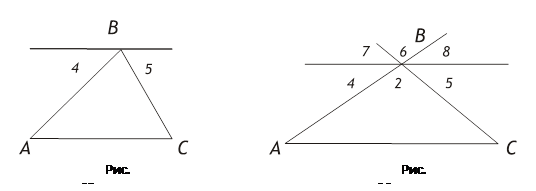
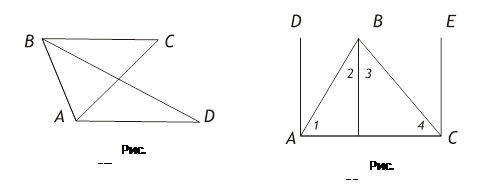
Учитель может для обобщающего урока заготовить четыре чертежа (рис. 35 — 36), по которым учащимся будет предложено доказать теорему о сумме углов треугольника. Доказательства, проводимые по каждому из рисунков, подключают каждый раз другой набор знаний, полученных школьниками в этой теме.