О взаимосвязях алгебры с геометрией

1.Требование метрической точности (наличие числового соответствия между предложенной задачей и чертежом) должно быть выполнено во всех случаях.

2. Следует уделять особое внимание наклону прямых. Под «наклоном» нужно понимать то же, что угловой коэффициент, т. е. тангенс угла, который прямая образует с осью Ох. Для учащихся, еще не знающих тригонометрии, ; «наклон» есть коэффициент при х в уравнении, решенном относительно у; чтобы увидеть его на чертеже, достаточно найти на прямой две «вершинки» (лучше — соседние) и, выделив прямоугольный треугольник с катетами, параллельными осям, для которого отрезок между «вершинками» служит гипотенузой, взять (с учетом знака) отношение вертикального катета к горизонтальному.

3. Необходимо добиться умения находить отрезки, которые прямая образует на координатных осях.

4. Наиболее трудным для усвоения является навык: провести прямую через две точки с заданными числовыми координатами. В уравнении у=ах+b буквенные коэффициенты а и b следует считать неизвестными и подбирать их значения в соответствии с требованиями задачи: получается линейная система.

Свойства трехчлена второй степени (в 8 классе) должны быть рассматриваемы в теснейшей связи с его графиком.

После рассмотрения в 8 классе графика функции у= может быть в порядке обобщения рассмотрен график дробной линейной функции

с числовыми коэффициентами; этот график строится учащимися по точкам в порядке упражнений. В результате построения учащиеся увидят, что график дробной линейной функции есть уже знакомая им кривая — гипербола. Вслед за этим учитель покажет учащимся, что построение графика дробной линейной функции легче выполнить после некоторых преобразований. Именно: для построения графика функции

предварительно выполняются следующие преобразования:

а) выделяется из дроби целая часть:

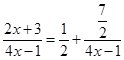
б) выносится за скобки коэффициент при х в знаменателе и записывается результат в виде:

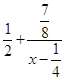
Теперь ясно видно, что график данной функции может быть получен из графика функции

путем перенесения последнего вправо на единицы масштаба и вверх на единицы масштаба; асимптотами перенесенного графика будут служить прямые, полученные путем перенесения оси ординат и оси абсцисс соответственно на -т единицы масштаба вправо и на единицы масштаба вверх; поэтому построение графика данной функции сводится к построению графика функции , отнесенного к прямым и как к осям.

В 9 классе следует уделить внимание графикам показательной и логарифмической функции.

Преподаватель должен во время работы с графиками функций следить за правильным пониманием и активным употреблением учащимися терминов, относящихся к возрастанию и убыванию функций. Надо, чтобы учащиеся, постепенно осваиваясь с этими терминами, употребляли их в более сокращенной редакции. Например, сначала, глядя на чертеж, следует «поведение» функции

у=х2—6x +11

характеризовать словами: «при возрастании переменной х от 3 до бесконечности функция у возрастает от 2 до бесконечности, а при возрастании переменной х от минус бесконечности до 3 функция у убывает от бесконечности до 2; в дальнейшем можно говорить короче: «функция у возрастает при x>3 от 2 до +¥ и убывает при х<;3 от +¥ до 2». «При х=3 функция у принимает наименьшее значение 2», или «достигает минимум 2».

Следует отметить, что важное значение имеют и геометрические задачи, которые сводятся к решению уравнений, можно проиллюстрировать такими задачами.

Сущность слияния областей математики может быть показанa и в следующих примерах.

Задача. В игре «Зарница» участвовало 72% всех школьников города. Из числа участников 60% были мальчики, а остальные, на которых приходилось 9000 человек, — девочки. Сколько школьников не участвовало в игре?

Данные задачи можно занести в таблицу